Relation Extraction Downstream Task를 어떻게 수행할 수 있을지 고민하다가 SPN논문을 찾아보게 되었다. Joint Entity and Relation Extraction 관련 포스트는 여기에서 확인할 수 있다.

1. Introduction

기존 Seq2Seq 기반 모델의 문제점

SPN_1

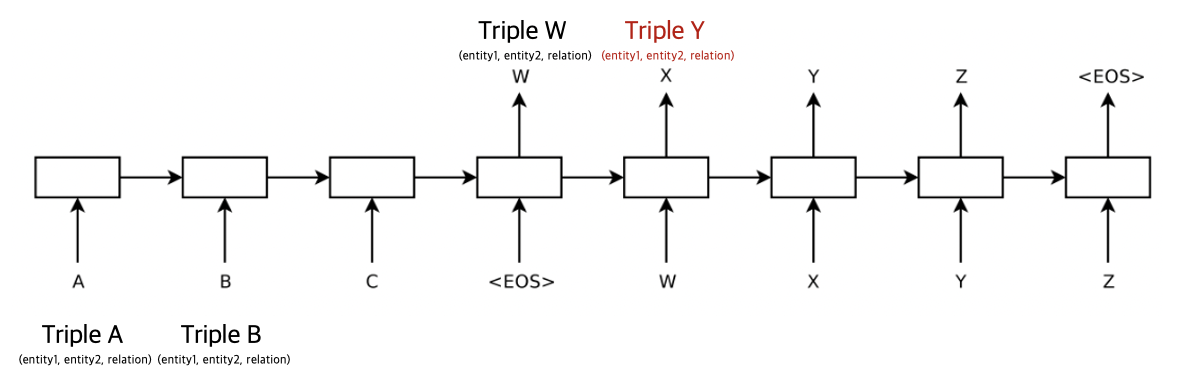
Seq2Seq Autoregressive Decoder와 Cross Entropy Loss는 다음과 같은 문제가 있음.

  1. Relation Extraction의 Triple Set에는 순서가 없지만 Autoregressive Decoder에는 정렬해서 입력해야 함
  2. Cross Entropy Loss는 순서에 민감함. 다른 위치에 생성된 모든 Triple에 대해 페널티를 부여하는 문제가 있음

위의 문제로 Seq2Seq 기반 모델은 Triple의 생성뿐만 아니라 그 생성 순서에 대해서도 모두 학습해야 한다.

Contributions

  1. Joint Entity and Relation Extraction Task를 Set Prediction Problem(집합 예측 문제)으로 하여 해결한다.
  2. Set Prediction Problem은 Non-Autoregressive Decoder와 Bipartite Matching Loss로 하여 해결한다.
  3. 두 개의 벤치마크 데이터셋에 대해 SOTA 결과 달성 + 위 두 방법의 효과에 대해 실험

2. Method

Notations

  • $X$ : raw sentence
  • $Y = {(s_1, r_1, o_1), … , (s_n, r_n, o_n)}$ : target triple set
\[P(Y|X) = p_L(n|X) \prod_{i=1}^{n} p(Y_i|X,Y_{i \ne j} ; \theta)\]
  • $p_L(n|X)$ : target triple set 크기 = triple 몇 개 생성할지
  • $p(Y_i|X,Y_{i \ne j} ; \theta)$ : target triple $Y_i$가 주어진 문장 $X$뿐만 아니라 다른 target triple $Y_{i \ne j}$와도 관련이 있음

Main Architecture

Architecture

Sentence Encoder

Goal

  • 각 token들의 context-aware represenation 얻음

output

  • token들의 context-aware representation $H_e \in \mathbb{R}^{l \times d}$
  • $l$ : 문장의 길이([CLS], [SEP] token 포함)
  • $d$ : Hidden State 크기

Non-Autoregressive Decoder for Triple Set Generation

Input

  • Decoding 전 Decoder는 target triple set의 크기를 알아야 함
  • $p_L(n|X)$ 먼저 모델링
    • $p_L(n|X)$ : 상수로 간단히 만듦
    • Non-Autoregressive Decoder가 각 문장마다 $m$만큼의 고정된 크기의 set 만듦
    • 단 $m$은 문장의 triple 개수보다 충분히 커야함
  • Decoder Input은 $m$개의 학습 가능한 Embedding(Triple Queries)로 초기화 : $\mathbb{R}^{m \times d}$
  • 모든 문장은 같은 Triple Queries 공유

Architecture

  • N개의 동일한 Transformer Layer
  • Multi-Head Self Attention : triple 간의 관계 모델링
  • Multi-Head Inter Attention : 주어진 문장의 정보를 혼합

  • $m$개의 Triple Queries는 $m$개의 Output Embedding으로 변환됨 : $H_d \in \mathbb{R}^{m \times d}$

  • FFN은 $H_d$를 Relation Types와 Entity로 독립적으로 Decode
  • $H_d$ 안의 Output Embedding $h_d \in \mathbb{R}^d$

Predicted Relation Type

  • $\mathbf{p}^r = \mathrm{softmax}(\mathbf{W}_\mathbf{r}\mathbf{h}_d)$
  • $\mathbf{W}_r \in \mathbb{R}^{t \times d}$, $t$ : relation types의 총 개수($\varnothing$ 포함)

Predicted Entity(subject, object)

  • 4개의 $l-class$ classifier로 index 예측
  • $\mathbf{p} ^{s-start}=\mathrm{softmax} (\mathbf{v}^T_1 \tanh(\mathbf{W}_{\mathbf{1}} \mathbf{h} _{\mathbf{d}} + \mathbf{W} _{\mathbf{2}}\mathbf{H} _{\mathbf{e}} ))$
  • $\mathbf{p} ^{s-start}=\mathrm{softmax} (\mathbf{v}^T_2 \tanh(\mathbf{W}_{\mathbf{3}} \mathbf{h} _{\mathbf{d}} + \mathbf{W} _{\mathbf{4}}\mathbf{H} _{\mathbf{e}} ))$
  • $\mathbf{p} ^{s-start}=\mathrm{softmax} (\mathbf{v}^T_3 \tanh(\mathbf{W}_{\mathbf{5}} \mathbf{h} _{\mathbf{d}} + \mathbf{W} _{\mathbf{6}}\mathbf{H} _{\mathbf{e}} ))$
  • $\mathbf{p} ^{s-start}=\mathrm{softmax} (\mathbf{v}^T_4 \tanh(\mathbf{W}_{\mathbf{7}} \mathbf{h} _{\mathbf{d}} + \mathbf{W} _{\mathbf{8}}\mathbf{H} _{\mathbf{e}} ))$
  • $\{ \mathbf{v} _i \in \mathbb{R}^d \} _{i=1}^4$, $\{\mathbf{W} _i \in \mathbb{R}^{d \times d}\} _{i=1}^8$

Bipartite Matching Loss

Notations

  • $ \mathbf{Y} = \{\mathbf{Y}_i\}^n _{i=1}$
    • ground truth triples, 나중에 $m$의 크기로 $\varnothing$으로 padding
  • $ \hat{\mathbf{Y}} = \{ \hat{\mathbf{Y}}_i \}^m _{i=1}, m>n $
  • $\mathbf{Y}_i = (r_i, s^{start}_i, s^{end}_i, o^{start}_i, o^{end}_i)$
    • $r_i$ - target relation type, $\varnothing$일수도 있음
    • $s^{start}_i, s^{end}_i, o^{start}_i, o^{end}_i$ : subject, object entity의 각 시작/끝 index
  • $\hat{\mathbf{Y}}_i = (\mathbf{p}^r_i, \mathbf{p}^{s-start}_i, \mathbf{p}^{s-end}_i, \mathbf{p}^{o-start}_i, \mathbf{p}^{o-end}_i)$

Loss

두 가지 step을 통하여 Loss를 구함

  1. Finding Optimal Matching
  2. Computing Loss Function

1. Finding Optimal Matching

\(\pi^* = \mathrm{arg} \min_{\pi \in \Pi(m)}\sum_{i=1}^m \mathcal{C}_{match}(\mathbf{Y}, \hat{\mathbf{Y}}_{\pi(i)})\)

  • $\pi(m)$ : 모든 $m$길이의 permuation space
\[\begin{aligned} \mathcal{C}_{match}(\mathbf{Y}, \hat{\mathbf{Y} _{\pi(i}}) = - \mathbb{l} _{r_i \neq \varnothing}[\mathbf{p}^{r} _{\pi(i)}(r_i) &+ \mathbf{p}^{s-start} _{\pi(i)}(s^{s-start}_i) + \mathbf{p}^{s-end} _{\pi(i)}(s^{s-end}_i)\\\\\\ &+ \mathbf{p}^{o-start} _{\pi(i)}(o^{o-start}_i) + \mathbf{p}^{o-end} _{\pi(i)}(o^{o-end}_i)] \end{aligned}\]
  • $\mathcal{C}_{match}(\mathbf{Y}, \hat{\mathbf{Y} _{\pi(i}})$ : pair-wise matching cost
    • Relation Type 예측과 Entity Span 예측을 모두 고려

예시

Aarhus airport serves the city of Aarhus , which is led by Jacob Bundsgaard .

  • 띄어쓰기를 기준으로 토큰 구분한다고 생각(index 0부터 매김)

  • Ground Truth

    $\mathbf{Y}_0 = \{0, 6, 6, 12, 13\}$
    $\mathbf{Y}_1 = \{1, 0, 1, 6, 6\}$
    $\mathbf{Y}_2 = \{3\}$

  • Predicted

    SPN_2

  • $\mathcal{C}_{match}$ 계산

    SPN_3

    SPN_4

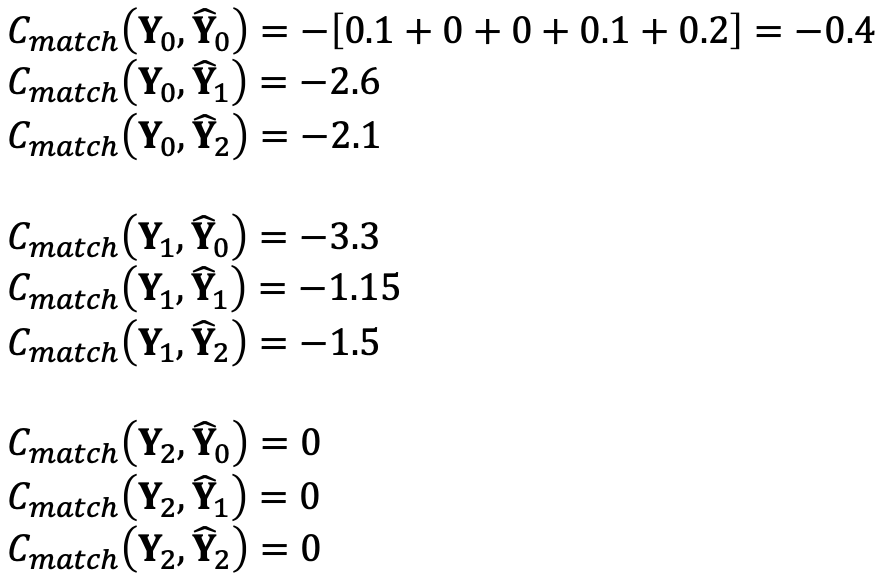
    이런 식으로 모든 경우에 대해 값을 계산한다.

  • cost matrix

    위에서 구한 값들로 cost matrix를 생성

    SPN_5

    Hungarian Algorithm으로 optimal assignment인 $\pi^*$ 구한다.

    $ground - truths : [0,1,2] \rightarrow prediction : [1,0,2]$

2. Computing the Loss Function

SPN_7

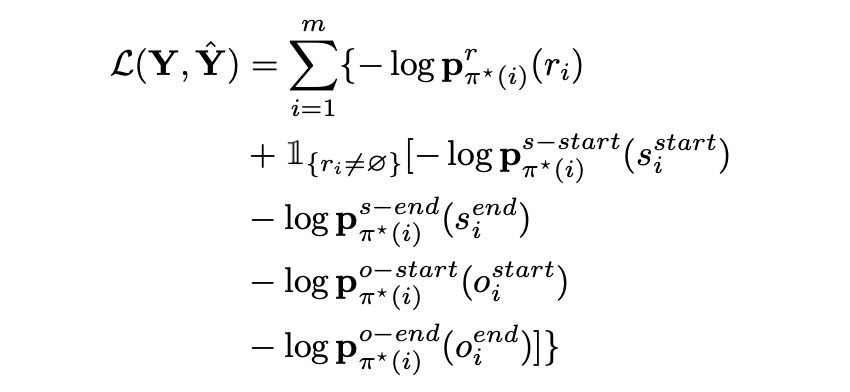
optimal assignment를 적용하여 loss 계산

SPN_6

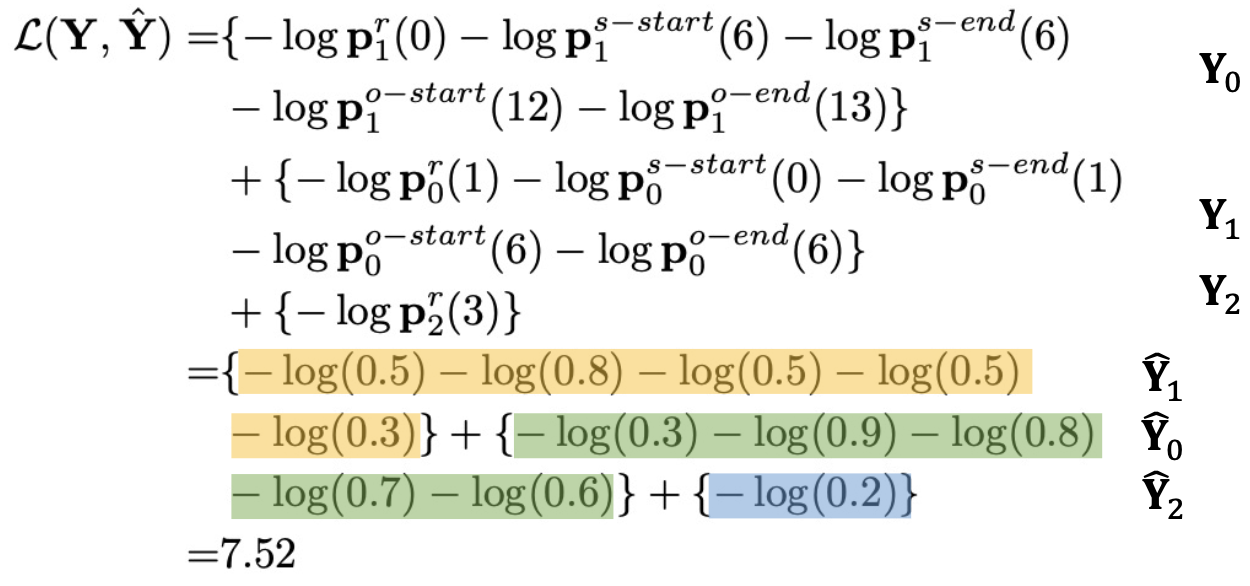
Conclusion

먼저 저번 포스트에 적었던 FinRED 데이터 문제를 해결해야 한다.
최대 512개를 넘는 문장들에 대해서 (subject, relation, object)의 각 entity가 512 내에 존재하는지에 대해 알아야 하며
특정 entity는 여러 단어가 조합된 경우 ‘+’를 추가한 경우가 있어 이에 대한 문제를 SPN이 해결할 수 있도록 하는 게 주 과제가 될 것 같다.

References